Inspirados já nos ensinamentos de Sófocles, aqui, procurar-se-á a conexão, pelo conhecimento, entre o velho e o novo, com seus conflitos. As pistas perseguidas, de modos específicos, continuarão a ser aquelas pavimentadas pelo grego do período clássico (séculos VI e V a.C).
sábado, 1 de janeiro de 2022
Estatísticas, Probabilidades e Esperanças
Conte comigo
***
https://www1.folha.uol.com.br/cotidiano/2021/12/mega-da-virada-deve-pagar-r-370-milhoes.shtml
Conte com a Sorte
mas saiba que sempre pode
Contar Comigo
***
A ESTATÍSTICA SERVE PARA FAZER COM QUE NÚMEROS SIMULEM O QUE SERIAM VERDADES VERDADEIRAS
********************************
Mega da Virada é dividida por apostas de Campinas (SP) e Cabo Frio (RJ)
Quem acertou os números 12, 15, 23, 32, 33 e 46 levará prêmio de R$ 378 milhões, o maior da história das Loterias da Caixa
31.dez.2021 às 17h15
Atualizado: 31.dez.2021 às 21h48
***
***
********************************************************************************************
***
***
sexta-feira, 31 de dezembro de 2021
Celso Ming: As incertezas e projeções para 2022
O Estado de S. Paulo.
De profeta e louco todo mundo tem um pouco, diz o ditado modificado para este texto. A cada fim de ano, a demanda por previsões aumenta. Mas é difícil separar o que são previsões propriamente ditas de meros votos ou de apostas.
Quem olha para a tabela ao lado verifica que até mesmo consultores tarimbados e gente graúda que põe dinheiro grosso a prazo, como a que está reunida pelo Banco Central, podem fracassar nas projeções. As que estão sendo feitas agora para o ano de 2022 parecem ainda mais sujeitas a erros.
De positivo para os próximos 12 meses, há as contas externas que deverão continuar excelentes. As reservas estão a US$ 364,2 bilhões, quase dois anos de importações. A produção do setor agropecuário será recorde e contribuirá para mais exportações. E certo grau de normalização dos fluxos globais de comércio também parece inevitável.
No entanto, o novo ano nasce carregado de três grandes incertezas e de outras, derivadas dessas. Uma delas é a evolução da pandemia. Ninguém sabe quanto o Brasil e o mundo estão sujeitos a novas evoluções do vírus. Faz um mês que as autoridades da África do Sul anunciaram o aparecimento da variante Ômicron e, no entanto, os infectologistas ainda não conhecem o suficiente da sua natureza. O que se pode dizer é que a população do Brasil e de grande número de países avançam na vacinação. A partir dessa mega incerteza, já não se sabe se voltará a ser necessário paralisar a atividade econômica e o quanto os fluxos de produção e comércio voltarão a se desorganizar.
A outra grande incerteza, desta vez específica do Brasil, é de natureza fiscal. O governo e o Congresso furaram o teto de gastos e oficializaram certo calote no resgate dos precatórios. Estão abertas as portas para toda a sorte de despesas eleitoreiras.
E aí chegamos à terceira maior incerteza. Sabe-se lá o que o presidente Bolsonaro aprontará para tentar convencer o eleitor a clicar seu voto na sua candidatura. Se confirmado o favoritismo das esquerdas, também poderá aparecer insegurança.
Derivadas dessas, vêm mais incertezas. São elas: o comportamento da economia global, a atuação dos grandes bancos centrais no enxugamento de recursos despejados na crise, a trajetória do câmbio e da inflação, o nível dos investimentos, o desempenho do PIB e o desemprego.
Apesar desses e outros pesares, feliz ano-novo. •
***
***
Não Custa Nada Tentar
***
***
Saber perder na vida é uma grande virtude
Cada sorriso um novo sonho
Cada sonho uma nova história
Encontrar lugares onde tudo pode acontecer
Saber na verdade o que é amar
Plantar os frutos da nossa missão
Saber que nunca vou te esquecer
Se te junto ao meu corpo
Se eu falo que te quero
Você sempre da seu jeito de fugir
Quando digo que te espero
Quando quero ser sincero
Você nunca quer me ouvir
Viver a vida
Com quem te faz feliz
Viva seus dias
Com quem te faz feliz
Dividir as escolhas
Praticar as idéias
Realizar os desejos traçados
Com alguém que te faz tão bem
Procurar entender
Que pra alcançar a nossa paz
É preciso saber ouvir
Se eu te olho em seus olhos
Se te peço que acredite
Pois na vida é assim
Sei que não sou perfeito
Me complete como homem
E se torne uma mulher pra mim
(Refrão)
Viver a vida
Com quem te faz feliz
Viva seus dias
Com quem te faz feliz
Procurar um sonho bom não é mal pra ninguém
No mundo não há quem te quis tão bem
Como eu quis você
Agora vem que eu te espero
Amor
Não custa nada tentar
Ouvir "Não Custa Nada Ten…"
******************************************************************
"O valor da aposta simples, com 6 números, é R$ 4,50."
***
***
Probabilidade - Quais São as Chances de Ganhar na Mega Sena? | Matemática Rio
24.194 visualizações29 de dez. de 2012
Matemática Rio com Prof. Rafael Procopio
***
Mega da Virada: número 10 foi o mais sorteado até hoje no concurso especial; confira outros
Próxima edição será realizada nesta sexta-feira com prêmio estimado de R$ 350 milhões, o maior da história da loteria
O Globo
29/12/2021 - 06:23 / Atualizado em 29/12/2021 - 06:28
***
***
Mega-sena da Virada Foto: Agência Brasil
Mega-sena da Virada Foto: Agência Brasil
***
RIO — Faltam apenas dois dias para o sorteio da Mega da Virada, que oferece a maior bolada do ano e da história da loteria: um prêmio estimado em R$ 350 milhões. Para ganhar a premiação, alguns apostadores contam com a sorte, mas também procuram saber quais as dezenas foram mais sorteadas no concurso especial criado em 2009.
Vídeo: Homem é mantido algemado e torturado em supermercado por suspeita de furto no MA
Neste período, foram realizados 12 sorteios da Mega da Virada. O número 10 foi o mais sorteado: quatro vezes, de acordo com divulgação da Caixa à imprensa.
Em seguida, as dezenas mais sorteadas são 03, 05, 20 e 36. Todos esses números saíram três vezes nos concursos especiais das loterias Caixa.
Ao todo, 16 dezenas foram sorteadas duas vezes desde que a Mega da Virada começou a ser realizada. São elas: 02, 11, 17, 18, 33, 34, 35, 37, 38, 40, 41, 42, 51, 53, 56 e 58.
Outras 22 dezenas saíram uma vez na Mega da Virada, segundo o Valor Investe: 01, 04, 06, 12, 14, 16, 24, 25, 27, 29, 30, 31, 32, 43, 45, 46, 47, 49, 50, 52, 55, 57.
Há, ainda, 16 números que jamais foram sorteados no concurso especial. Tome nota: 07, 08, 09, 13, 15, 19, 21, 23, 26, 28, 39, 44, 48, 54, 59, 60.
Simples, curtos e bíblicos: veja o perfil de nomes mais escolhidos pelos brasileiros em 2021
As casas lotéricas e plataformas digitais da Caixa já estão recebendo apostas desde o dia 16 de novembro. A Caixa Econômica Federal fará o sorteio milionário no dia 31 de dezembro. O concurso será o de número 2.440 e até lá não haverá mais sorteios.
Por se tratar de um concurso especial, o prêmio não acumula. Caso não haja acerto para as seis dezenas, o valor será dividido entre os acertadores de cinco dezenas. O valor prometido é maior do que o de 2020, quando a Caixa estimou o prêmio em R$ 300 milhões.
As apostas podem ser feitas nas casas lotéricas de todo o país, pelo aplicativo Loterias Caixa ou pela internet. O valor da aposta simples, com
Desaparecido nos EUA: Homem que procurava chifres de veado em floresta encontra restos mortais de lutador de MMA
Estimativas feitas pela Caixa mostram que caso o sortudo leve a bolada sozinho, se aplicado o dinheiro na poupança, terá um rendimento de R$ 1,5 milhão mensais, o total é dinheiro suficiente ainda para comprar 40 mansões de R$ 8,75 milhões, cada.
Bolões
Para aumentar as chances de ganhar, muitos jogadores optam por adquirir cotas dos bolões, já que concorrem com uma maior quantidade de jogos e de números em uma aposta, gastando menos.
Para realizar o bolão, basta formar um grupo, escolher os números da aposta, marcar a quantidade de cotas e registrar em qualquer uma das 13 mil lotéricas do país. Ao ser registrada no sistema, a aposta gera um recibo de cota para cada participante que, em caso de premiação, poderá resgatar o prêmio individualmente.
Nova CNH: Saiba como ficará a carteira de motorista a partir de 2022
O apostador também pode adquirir cotas de bolões organizados pelas lotéricas. Para isso, é preciso solicitar ao atendente a quantidade de cotas que deseja e guardar o recibo para conferir a aposta no dia do sorteio. Nesse caso, poderá pagar uma tarifa de serviço adicional de até 35% do valor da cota, a critério da lotérica.
Na Mega-Sena, os bolões têm preço mínimo de R$ 10. Porém, cada cota não pode ser inferior a R$ 5. É possível realizar um bolão de no mínimo 2 e no máximo 100 cotas. É permitida a realização de no máximo 10 apostas por bolão. Nos casos de mais de uma aposta, todas elas deverão conter a mesma quantidade de números de prognósticos.
Como acompanhar o sorteio
O concurso 2440 será realizado a partir das 20h (horário de Brasília) com transmissão ao vivo pela internet, no canal oficial da Caixa no YouTube. O sorteio será transmitido também diretamente dos estúdios da TV GLOBO como já é tradição. (Com informações da Agência Brasil)
SAIBA MAIS
BRASIL
Brasil terá nova carteira de motorista em 2022: saiba como será o novo modelo
Nova Carteira Nacional de Habilitação Foto: Reprodução
BRASIL
Simples, curtos e bíblicos: veja o perfil de nomes mais escolhidos pelos brasileiros em 2021
Estudo aponta que bebês que dormem por mais tempo e com menos interrupções têm menos risco de sobrepeso. Foto: Unsplash
CULTURA
Marília Mendonça, Paulo Gustavo e Tarcísio Meira: relembre famosos mortos em 2021
Marília Mendonça, Paulo Gustavo e Tarcísio Meira Foto: Reprodução
BRASIL
Mega da Virada: Apostadores têm até as 17h desta sexta-feira para tentar prêmio inédito de R$ 350 milhões
Mega-sena da Virada Foto: Agência Brasil
O GLOBO RECOMENDA
BRASIL
'Lá vem o aluno com seu travequinho'; atleta trans revela ameaças após formatura de namorado militar
Foto da Recomendação
MUNDO
Vidente que previu o 11 de setembro e a morte da princesa Diana diz que haverá uma nova pandemia em 2022
Foto da Recomendação
***********************************
***
A Matemática da Mega da VIRADA
518.323 visualizações30 de dez. de 2019
13 MIL
******************************************************
Equaciona Com Paulo Pereira
Quer saber p que fazer pra ganhar com certeza na mega da virada? Assista até o final. É possível! Mas você precisa já ser milionário hehe...
FELIZ 2020!!
BOA SORTE!!
**********************************
MATEMÁTICA
Estatística
A estatística é o campo da matemática que relaciona fatos e números em que há um conjunto de métodos que nos possibilita coletar dados e analisá-los, assim sendo possível realizar alguma interpretação deles. A estatística é dividida em duas partes: descritiva e inferencial. A estatística descritiva é caracterizada pela organização, análise e apresentação dos dados, enquanto a estatística inferencial tem como característica o estudo de uma amostra de determinada população e, com base nela, a realização de análises e a apresentação de dados.
Leia também: O que é margem de erro de uma pesquisa?
Princípios da estatística
Veremos, a seguir, os principais conceitos e princípios da estatística. Com base neles, será possível definir conceitos mais sofisticados.
População ou universo estatístico
A população ou universo estatístico é o conjunto formado por todos elementos que participam de um determinado tema pesquisado.
Exemplos de universo estatístico
a) Em uma cidade, todos os habitantes pertencem ao universo estatístico.
b) Em um dado de seis faces, a população é dada pelo número de faces.
{1, 2, 3, 4, 5, 6}
Dado estatístico
O dado estatístico é um elemento que pertence ao conjunto da população, obviamente esse dado deve estar envolvido com o tema da pesquisa.
População
Dado estatístico
Dado de seis faces
4
Campeões Brasileiros de Mountain Bike
Henrique Avancini
Amostra
Chamamos de amostra o subconjunto formado com base no universo estatístico. Uma amostra é utilizada quando a população é muito grande ou infinita. Em casos em que coletar todas as informações do universo estatístico é inviável por motivos financeiros ou logísticos, também se faz necessário a utilização de amostras.
A escolha de uma amostra é de extrema importância para uma pesquisa, e ela deve representar de maneira fidedigna a população. Um exemplo clássico da utilização das amostras em uma pesquisa é na realização do censo demográfico do nosso país.
Variável
Em estatística, a variável é o objeto de estudo, isto é, o tema que a pesquisa pretende estudar. Por exemplo, ao estudar-se as características de uma cidade, o número de habitantes pode ser uma variável, assim como o volume de chuva em determinado período ou até mesmo a quantidade de ônibus para o transporte público. Note que o conceito de variável em estatística é dependente do contexto da pesquisa.
A organização dos dados em estatística dá-se em etapas, como em todo processo de organização. Inicialmente é escolhido o tema a ser pesquisado, em seguida, é pensado o método para a coleta dos dados da pesquisa, e o terceiro passo é a execução da coleta. Após o fim dessa última etapa, faz-se a análise do que foi coletado, e assim, com base na interpretação, busca-se resultados. Veremos, agora, alguns conceitos importantes e necessários para a organização dos dados.
Rol
Em casos em que os dados podem ser representados por números, ou seja, quando a variável é quantitativa, utiliza-se o rol para organização desses dados. Um rol pode ser crescente ou decrescente. Caso uma variável não seja quantitativa, ou seja, caso seja qualitativa, não é possível utilizar-se o rol, por exemplo, se os dados são sentimentos sobre determinado produto.
Exemplo
Em uma sala de aula, foram coletadas as alturas dos alunos em metros. São elas: 1,70; 1,60; 1,65; 1,78; 1,71; 1,73; 1,72; 1,64.
Como o rol pode ser organizado de maneira crescente ou decrescente, segue que:
rol: {1,60; 1,64; 1,65; 1,70; 1,71; 1,72; 1,73; 1,78}
Observe que, com o rol já montado, é possível encontrar um dado com mais facilidade.
Tabela de distribuição de frequência
Em casos nos quais há muitos elementos no rol e muitas repetições de dados, o rol torna-se obsoleto, pois a organização desses dados é inviável. Nesses casos, as tabelas e a distribuição de frequências servem como uma excelente ferramenta de organização.
Na tabela de distribuição de frequência absoluta, devemos colocar a frequência em que cada dado aparece, ou seja, a quantidade de vezes que ele aparece.
Vamos construir a tabela de distribuição de frequência absoluta das idades, em anos, dos alunos de uma determinada classe.
Distribuição de frequências absolutas
Idade
Frequência (F)
8
2
9
12
10
12
11
14
12
1
Total (FT)
41
Da tabela podemos obter as seguintes informações: na classe temos 2 alunos com a idade de 8 anos, 12 alunos com 9 anos, e mais 12 alunos com 10 anos, e assim sucessivamente, alcançando o total de 41 alunos. Na tabela de distribuição de frequências acumuladas, devemos somar a frequência da linha anterior (na tabela de distribuição de frequência absoluta).
Vamos construir a tabela de distribuição de frequência acumulada das idades da mesma classe do exemplo anterior, veja:
Distribuição de frequências acumuladas
Idade
Frequência (F)
8
2
9
14
10
26
11
40
12
41
Total (FT)
41
Na tabela de distribuição de frequências relativas, utiliza-se a porcentagem em que cada dado aparece. Novamente faremos os cálculos baseados na tabela de distribuição de frequência absoluta. Sabemos que 41 corresponde a 100% dos alunos da classe, logo, para determinar a porcentagem de cada idade, basta dividirmos a frequência da idade por 41 e multiplicarmos o resultado por 100, para, assim, escrevermos na forma de porcentagem.
2 : 41 = 0,048 · 100 → 4,8%
12 : 41 = 0,292 · 100 → 29,2%
12 : 41 = 0,292 · 100 → 29,2%
14 : 41 = 0,341 · 100 → 34,1%
1 : 41 = 0,024 · 100 → 2,4%
Distribuição de frequências relativas
Idade
Frequência (F)
8
4,8%
9
29,2%
10
29,2%
11
34,1%
12
2,4%
Total (FT)
100%
Leia também: Aplicação de estatística: frequência absoluta e frequência relativa
Classes
Em casos em que a variável é contínua, isto é, quando ela possui diversos valores, é necessário agrupá-los em intervalos reais. Na estatística esses intervalos são chamados de classes.
Para construir a tabela de distribuição de frequências em classes, devemos colocar os intervalos na coluna da esquerda, com seu devido título, e na coluna da direita, devemos colocar a frequência absoluta de cada um dos intervalos, ou seja, quantos elementos pertencem a cada um deles.
Exemplo
Altura dos alunos da classe do 3º ano do Ensino Médio de uma escola.
Distribuição de frequência em classes
Altura (metros)
Frequência absoluta (F)
[1,40; 1,50[
1
[1,50; 1,60[
4
[1,60; 1,70[
8
[1,70; 1,80[
2
[1,80; 1,90[
1
Total (FT)
16
Analisando a tabela de distribuição de frequência em classes, podemos ver que, na turma do terceiro ano, temos 1 estudante que possui altura entre 1,40 m e 1,50 m, assim como temos 4 estudantes com altura entre 1,50 e 1,60 m, e assim sucessivamente. Podemos observar também que os estudantes possuem altura entre 1,40 m e 1,90 m, a diferença entre essas medidas, ou seja, entre a maior altura e a menor altura da amostra, é chamada de amplitude.
A diferença entre o limite superior e o limite inferior de uma classe é chamada de amplitude da classe, assim, a segunda, que possui 4 alunos com alturas entre 1,50 metro (inclusos) e 1,60 metro (não inclusos), possui amplitude de:
1,60 – 1,50
0,10 metro
Veja também: Medidas de dispersão: amplitude e desvio
Medidas de posição
As medidas de posição são utilizadas em casos em que é possível construir-se um rol numérico com os dados ou uma tabela de frequência. Essas medidas indicam a posição dos elementos em relação ao rol. As três principais medidas de posição são:
Média
Considere o rol com os elementos (a1, a2, a3, a4, …, an), a média aritmética desses n elementos é dada por:
Exemplo
Em um grupo de dança, as idades dos integrantes foram coletadas e representadas no rol a seguir:
(18, 20, 20, 21, 21, 21, 22, 22, 25, 30)
Vamos determinar a idade média dos integrantes desse grupo de dança.
De acordo com a fórmula, devemos somar todos os elementos e dividir esse resultado pela quantidade de elementos do rol, assim:
Portanto, a idade média dos integrantes é de 22 anos.
Para saber mais sobre essa medida de posição, leia nosso texto: Média.
Mediana
A mediana é dada pelo elemento central de um rol que possui uma quantidade ímpar de elementos. Caso o rol possua uma quantidade par de elementos, devemos considerar os dois elementos centrais e calcular a média aritmética entre eles.
Exemplo
Considere o rol a seguir.
(2, 2, 3, 3, 4, 5, 6, 7, 9)
Veja que o elemento 4 divide o rol em duas partes iguais, logo, ele é o elemento central.
Exemplo
Calcule a mediana das idades do grupo de dança.
Lembre-se de que o rol das idades desse grupo de dança é dado por:
(18, 20, 20, 21, 21, 21, 22, 22, 25, 30)
Veja que o número de elementos desse rol é igual a 10, logo, não é possível dividir o rol em duas partes iguais. Assim devemos tomar dois elementos centrais e realizar a média aritmética desses valores.
Veja mais detalhes dessa medida de posição em nosso texto: Mediana.
Moda
Chamaremos de moda o elemento do rol que possui maior frequência, ou seja, o elemento que mais aparece nele.
Exemplo
Vamos determinar a moda do rol das idades do grupo de dança.
(18, 20, 20, 21, 21, 21, 22, 22, 25, 30)
O elemento que mais aparece é o 21, portanto, a moda é igual a 21.
Medidas de dispersão
As medidas de dispersão são utilizadas nos casos em que a média já não é suficiente. Por exemplo, imagine que dois carros tenham percorrido uma média de 40.000 quilômetros. Somente com conhecimento sobre média podemos afirmar que os dois carros andaram determináveis quilômetros cada um, certo?
No entanto, imagine que um dos carros tenha percorrido 79.000 quilômetros, e o outro, 1.000 quilômetros, veja que somente com as informações sobre média não é possível realizar afirmações com precisão.
As medidas de dispersão nos indicarão o quanto os elementos de um rol numérico estão afastados da média aritmética. Temos duas importantes medidas de dispersão:
Variância (σ2)
Vamos chamar de variância a média aritmética dos quadrados da diferença entre cada elemento do rol e a média aritmética desse rol. A variância é representada por: σ2.
Considere o rol (x1, x2, x3, …, xn) e que ele possua média aritméticax. A variância é dada por:
Desvio-padrão (σ)
O desvio-padrão é dado pela raiz da variância, ele nos indica o quanto um elemento está disperso em relação à média. O desvio padrão é denotado por σ.
Exemplo
Determine o desvio-padrão do conjunto de dados (4, 7, 10). Veja que, para isso, é necessário determinar-se primeiro a variância, e que, para tanto, é necessário antes o cálculo da média desses dados.
Substituindo esses dados na fórmula da variância, temos:
Para determinar o desvio-padrão, devemos extrair a raiz da variância.
Leia mais: Medidas de dispersão: variância e desvio-padrão
Para que serve a estatística?
Vimos que a estatística está relacionada a problemas de contagem ou organização de dados. Além disso, ela tem um importante papel no desenvolvimento de ferramentas que possibilitam o processo de organização de dados, com em tabelas. A estatística está presente também em diversos campos da ciência, com base na coleta de dados e em seu tratamento, é possível trabalhar modelos matemáticos que permitem maior desenvolvimento na área estudada. Alguns campos em que a estatística é fundamental: economia, meteorologia, marketing, esportes, sociologia e geociências.
Na meteorologia, por exemplo, os dados são coletados em determinado período, depois de organizados, eles são tratados, e assim, com base neles, constrói-se um modelo matemático que nos permite afirmar sobre o clima de dias anteriores com maior grau de confiabilidade. A estatística é um ramo da ciência que nos permite fazer afirmações com certo grau de confiabilidade, mas nunca com 100% de certeza.
Divisões da estatística
A estatística é dividida em duas partes, descritiva e inferencial. A primeira está relacionada à contagem dos elementos envolvidos na pesquisa, esses elementos são contados um a um. Na estatística descritiva, temos como principais ferramentas as medidas de posição, como média, mediana e moda, assim como as medidas de dispersão, como variância e desvio-padrão, temos também tabelas de frequências e gráficos.
Ainda na estatística descritiva, temos uma metodologia muito bem definida para uma apresentação de dados com grau considerável de confiabilidade que passa por organização e coleta, resumo, interpretação e representação e, por fim, análise de dados. Um exemplo clássico da utilização da estatística descritiva ocorre na realização do censo populacional (de 10 em 10 anos) pelo Instituto Brasileiro de Geografia e Estatística (IBGE).
A estatística inferencial, por sua vez, é caracterizada não por coletar dados dos elementos de uma população um a um, e sim por realizar a análise de uma amostra dessa população, tirando conclusões sobre ela. Na estatística inferencial, deve-se tomar cuidado na escolha da amostra, pois ela deve representar muito bem a população. Alguns resultados iniciais, como calculo de média, na estatística inferencial chamado de esperança, são deduzidos com base nos conhecimentos da estatística descritiva.
A estatística inferencial é utilizada, por exemplo, nas pesquisas eleitorais. Escolhe-se uma amostra da população, de forma que a represente, e assim é realizada a pesquisa. Na escolha de uma amostra que não represente muito bem essa população, dizemos que a pesquisa é tendenciosa e, por consequência, não confiável.
Área da matemática responsável pela contagem e pela organização de dados.
Área da matemática responsável pela contagem e pela organização de dados.
Exercícios resolvidos
Questão 1 – (U. F. Juiz de Fora – MG) Um professor de física aplicou uma prova, valendo 100 pontos, em seus 22 alunos e obteve, como resultado, a distribuição das notas, vista no quadro seguinte:
40
20
10
20
70
60
90
80
30
50
50
70
50
20
50
50
10
40
30
20
60
60
–
–
Faça os seguintes tratamentos de dados:
a) Escreva o rol dessas notas.
b) Determine a frequência relativa da maior nota.
Resolução
a) Para fazer o rol dessas notas, devemos escrevê-las de maneira crescente ou decrescente. Assim temos que:
10, 10, 20, 20, 20, 20, 30, 30, 40, 40, 50, 50, 50, 50, 50, 60, 60, 60, 80, 90
b) Observando o rol, podemos ver que a maior nota foi igual a 90 e que sua frequência absoluta é igual a 1, pois ela aparece apenas uma vez. Para determinar a frequência relativa, devemos dividir a frequência absoluta dessa nota pela frequência total, nesse caso, igual a 22. Assim:
Frequência relativa
Para passar esse número para porcentagem, devemos multiplicá-lo por 100.
0,045 · 100
4,5%
Questão 2 – (Enem) Depois de jogar um dado em forma de cubo e de faces numeradas de 1 a 6, por 10 vezes consecutivas, e anotar o número obtido em cada jogada, constituiu-se a seguinte tabela de distribuição de frequências.
Número obtido
Frequência
1
4
2
1
4
2
5
2
6
1
A média, a mediana e a moda dessa distribuição de frequências são, respectivamente:
a) 3, 2 e 1
b) 3, 3 e 1
c) 3, 4 e 2
d) 5, 4 e 2
e) 6, 2 e 4
Resolução
Alternativa B.
Para determinarmos a média, observe que existe repetição dos números obtidos, assim, utilizaremos a média aritmética ponderada.
Para determinar a mediana, devemos organizar o rol de maneira crescente ou decrescente. Lembre-se de que a frequência é a quantidade de vezes que a face aparece.
1, 1, 1, 1, 2, 4, 4, 5, 5, 6
Como o número de elementos do rol é par, devemos calcular a média aritmética dos elementos centrais que dividem o rol ao meio para determinar a mediana, assim:
A moda é dada pelo elemento que mais aparece, ou seja, que possui maior frequência, portanto, temos que a moda é igual 1.
Assim a média, a mediana e a moda são, respectivamente, iguais a:
3, 3 e 1
Por Robson Luiz
Professor de Matemática
Listagem de Artigos
Assista às nossas videoaulas
Vídeo 1Vídeo 2Vídeo 3Vídeo 4
Lista de Exercícios
Questão 1
Em um grupo de pessoas, as idades são : 10, 12, 15 e 17 anos. Caso uma pessoa de 16 anos junte-se ao grupo, o que acontece com a média das idades do grupo?
Questão 2
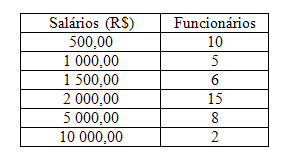
A distribuição de salários de uma empresa é fornecido pela tabela a seguir:
Calcule a média salarial dessa empresa.
Ver resposta
https://brasilescola.uol.com.br/matematica/estatistica-2.htm
**********************************************************************
***
A Matemática da Mega da VIRADA
518.323 visualizações30 de dez. de 2019
Equaciona Com Paulo Pereira
1,13 mi de inscritos
Quer saber p que fazer pra ganhar com certeza na mega da virada? Assista até o final. É possível! Mas você precisa já ser milionário hehe...
FELIZ 2020!!
BOA SORTE!!
https://www.youtube.com/watch?v=rS0ZmZdr__U
***************************************************
***
Curiosidades Matemáticas | Qual a chance de ganhar na Mega-Sena?
15.777 visualizações19 de nov. de 2015
***
Matemática em Exercícios
514 mil inscritos
Nesse primeiro vídeo da série curiosidades matemáticas vamos falar sobre probabilidade, num assunto que desperta muito interesse, o sorteio da Mega-Sena. Vamos calcular a probabilidade de ganhar na Mega-Sena acertando todos os 6 números com uma aposta simples e também com uma aposta máxima.
https://www.youtube.com/watch?v=x1MzRX5KXN0
Assinar:
Postar comentários (Atom)





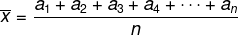
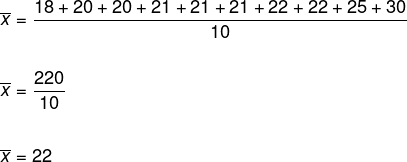
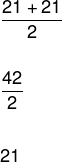
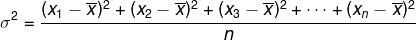
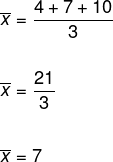
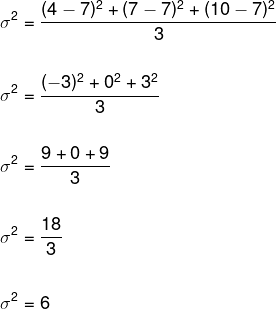
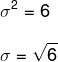
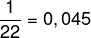
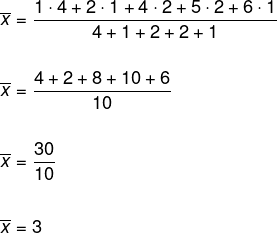
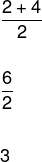
Nenhum comentário:
Postar um comentário